Summary of BatchNorm

What did the authors want to achieve ?

make normalization a part of the model
allow the use of higher learning rates by ensuring a stable distribution of nonlinear inputs => faster training, less iterations needed
improve robustness to initialization (more independent of good init) : reduce dependence of gradients on parameter scale and of the initial values
normalize the activations and preserve information in the network

Key elements

Old approaches

whitening (linearly transforming inputs to have zero mean and unit variance and beingdecorrelated), has several problems. If the whitening modifiactions are interspersed with the optimization technique, gradient descent might try to update the parameters in a way that needs the normalization to be updated as well. This greatly reduces the effect of the backward pass step. In the paper this is shown by using considering a layer and normalizing the result with the mean of the training data. (see picture above) The authors show that the bias b will grow indefinitely while the loss remains the same. This was also observed in experiments, where the model blew up when the normalization parameters where computed outside of the backward pass. This is due to that approach not considering that during gradient descent, the normalization is taking place.

Batch Norm

the idea is to normalize the activations during training, by normalizing the training samples (batches), relative to the statistics of the entire train set
- as normalization may change what the layer already represents (Sigmoid normalization would constrain it to the linear part in between the saturation), the inserted transformation needs to be able to represent an identity tansformation. This is done by introducing two new learnable parameters for each batch for scaling and shifting the normalized value :

With $\gamma ^{k} = \sqrt{Var[x^{k}]}$ and $\beta ^{k} = E[x^{k}]$, the original activation can be restored

for each mini-batch mean and covariance is computed seperately, therefore the name Batch Normalization, the small parameter eta is used in order to avoid division by zero, when the standard deviation is 0 (this could happen in case of bad init for example) :

BN can be applied to every activation (at least in feedforward networks and as long as there is a high enough batch size), as BN is differentiable, the chain rule can be used to consider the BN transformation :

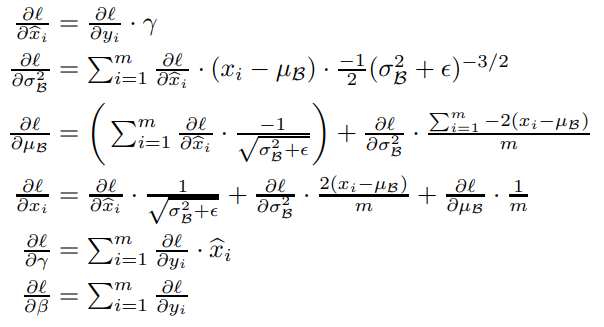
images

During training the following pseudocode applies :

During testing a running moving average of mean and variance is used (linear transform), as the normalization based on a mini-batch is not desirable
Batch Norm prevents small changes of parameters to amplify larger changes in our network. Higher learning rates also don't influence the scale of the parameters during backprop, therefore amplification is prevented as the layer Jacobian is unaffected. The singular values of the Jacobian are also close to 1, which helps preserve gradient magnitudes. Even though the transformation is not linear and the normalizations are not guaranteed to be Gaussian or independent, BN is still expected to improve gradient characterisitcs.

Implementation

Batch Norm can be implemented as follows in PyTorch : Also check out my summary of the Batch Norm part of the DL course by fastai for more normalization techniques such as running batch norm, layer and group norm, and a small Residual Net with Batch Norm. This is the same as the torch.nn module would do it, but it's always great to see it from scratch.

#collapse_show
class BatchNorm(nn.Module):
    def __init__(self, nf, mom=0.1, eps=1e-5):
        super().__init__()
        # NB: pytorch bn mom is opposite of what you'd expect
        self.mom,self.eps = mom,eps
        self.mults = nn.Parameter(torch.ones (nf,1,1))
        self.adds  = nn.Parameter(torch.zeros(nf,1,1))
        self.register_buffer('vars',  torch.ones(1,nf,1,1))
        self.register_buffer('means', torch.zeros(1,nf,1,1))

    def update_stats(self, x):
        #we average over all batches (0) and over x,y(2,3) coordinates (each filter)
        #keepdim=True means we can still broadcast nicely as these dimensions will be left empty
        m = x.mean((0,2,3), keepdim=True)  
        v = x.var ((0,2,3), keepdim=True)
        self.means.lerp_(m, self.mom)
        self.vars.lerp_ (v, self.mom)
        return m,v
        
    def forward(self, x):
        if self.training:
            with torch.no_grad(): m,v = self.update_stats(x)
        else: m,v = self.means,self.vars
        x = (x-m) / (v+self.eps).sqrt()
        return x*self.mults + self.adds

Results and Conclusion

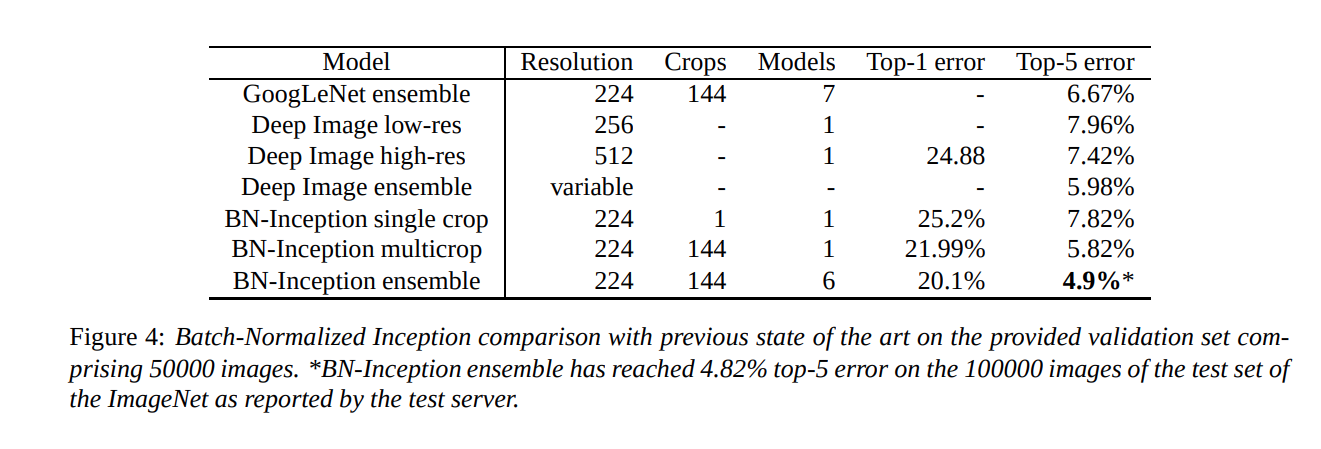
Batch Norm allows to use only 7% of the training steps to match previous state of the art models on ImageNet without it
Batch Norm Inception beats the state of the art on the ImageNet challenge
Batch Norm reduces the need for Dropput greatly as claimed by the authors, however it was still used with the traditional dropout set up used by the Inception architects