What did the authors want to achieve ?

Combat the deficits of Conolutional Architectures, (local connectivity, failing to reason globally) by introducing Attention to as a stand-alone layer. The authors prove that this can be both more accurate and more efficient at the same time. Architectures that are attention only, and a mixed version of convolutional and attention architectures are introduced and compared to the vanilla convolutional implementations.

Methods

Conv Block deficits

Capturing long range interactions is challenging for convolutions as they do not scale well with large receptives. Since attention has been used to tackle long range dependencies in sequence modeling, since architectures like SE Nets model attention on a chanel wise basis successfully. However in these cases attention was only an add-on to a traditional architecture style. In this paper the authors propose to use attention mechanisms as stand alone layers.

Self-Attention

Attention was originally introduced in order to allow for summarization from variable length source sentences. Attention focuses on the important parts of the input and thereby can serve as a primary representation learning mechanism and fully replace recurrence. The word self means that it just considers a single context (query,keys and values are extracted from the same image). The breakthrough in this paper is the use of self-attention layers instead of convolutional layers.

In this work, already existing mechanisms are used which are not optimized for the image domain. Therefore it is permutation equivariant and has limited expression capability for vision tasks.

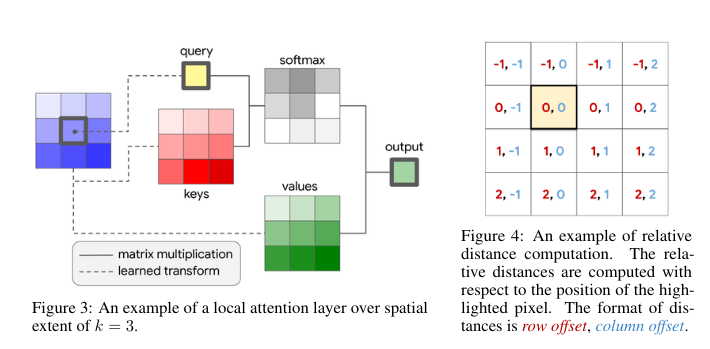
The process is as follows : 1) given a pixel $x_{i,j} \in R^{d_{in}}$ in positions $ab \in N_{k}(i,j)$ a local kernel with kernel size $k$ is extracted. $x_{i,j}$ is the middle of the kernel, which is called memory block. Prior work only performed global attention, which can only be done with a downsized sample as it is very compute expensive.

2) Single headed attention is computed :

$y_{i,j} = \sum_{ab \in N_{k}(i,j)} softmax_{a,b}(q_{ij}^{T}k_{ab})v_{ab}$

where the ${queries}$ $q_{ij} = W_Q x_{ij}$

${keys}$ $k_{ab} = W_K x_{ab}$

and ${values}$ $v_{ab} = W_V x_{ab}$

are linear transformations of the pixel in position and it's neighbors in the kernel.

$\texttt{softmax}_{a b}$ is a softmax, which is applied to all logits computed in the neighborhood of $ij$. $W_Q, W_K, W_V \in \mathbb{R}^{d_{out} \times d_{in}}$ are learned transforms.

Local self-attention is similar to convolution in the way that it aggregates spatial information in the neighborhoods, multi attention heads are used to learn unique representations of the input. This is done by partitioning pixel features into $N$ groups and then computing single-headed attention on each one seperately with the transforms $W_Q, W_K, W_V \in \mathbb{R}^{d_{out} \times d_{in}}$. The outputs of the heads are then concatenated.

2D relative pose embeddings,relative attention is used :

1) relative attention computes relative distances of the pixel to each one in the neighborhood : row $(a-i)$ and column offset $(b-j)$
2) row and column offset are associated with an embedding and concatenated into a vector $r_{a-i,b-j}$

3) Spatial-relative attention is then defined as :

$y_{ij} = \sum_{a,b\in N_{k}(i, j)} softmax_{ab}(q_{ij}^{T}k_{ab}+q_{ij}^{T}r_{a-i,b-j})v_{ab}$

The logit measuring similarity between the query and an element results from the content of the element and the relative distance of the element from the query. By inlcuding this spatial information, self-attention also has translation equivariance, just like conv layers. Unlike conv layers, self-attentions parameter count is independent of its spatial extent. The compute cost also grows slower : For example, if $d_{in} = d_{out} = 128$, a convolution layer with $k = 3$ has the same computational cost as an attention layer with $k = 19$.

Using this as their basis, a fully attentional architecture is created in two steps:

Replacing Spatial Convolutions

A spatial conv is defined to have spatial extent k > 1, which also includes 1x1 convolutions. These can be viewed as fully connected layers. Here the authors want to replace conv blocks in a straightforward way, specificially focusing on ResNet. Therefore the 3x3 convolution in Path B is swapped with a self-attention layer as defined above. All the other blocks are not changed, this might be supobtimal but promises potential improvements using architecture search.

Replacing the Convolutional Stem (intial layers of the CNN)

This part focuses on replacing the inital layers, as they are the most compute expensive due to the large input size of the image. In the OG ResNet the input is a 7x7 kernel with stride 2, followed by 3x3 max pooling with stride 2. At the beginning RGB pixels are individually uninformative and information is heavily spatially correlated through low level features such as edges. Edge detectors are difficult to learn for self-attention due to spatial correlation, convs learn these easily through distance based weight parameterization. The authors inject spatially-varying linear transforms into the pointwise 1x1 softmax convolution.

$\tilde{v}_{a b} = \left(\sum_m p(a, b, m) W_V^{m}\right) x_{a b}$

The results is similar to convolutions, weights are learned based on a local neighborhood basis. So in total the stem consists of spatially aware value features, followed by max-pooling. A more detailed explanation of this can be found in the appendix of the paper (page 14/15).

Results

Implementation details for both classification and object detection are in the appendix.

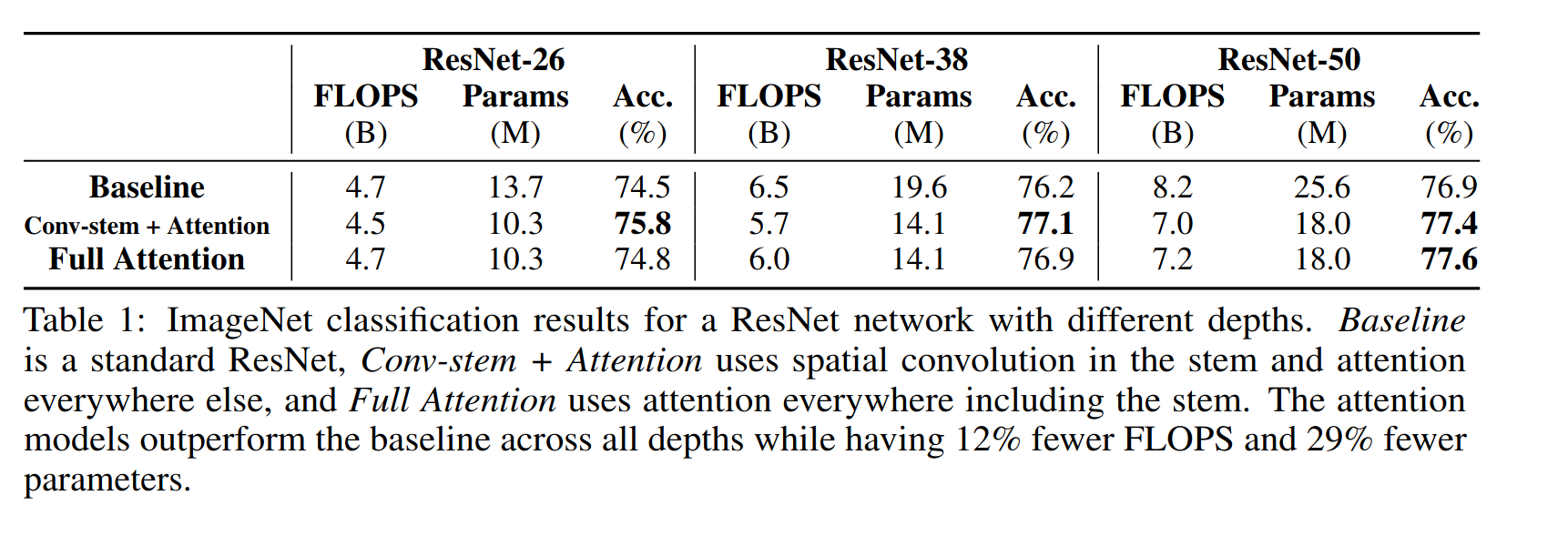
ImageNet

The multi head self-attention layer uses a spatial width of k=7 and 8 attention heads. The position-aware attention stem as described above is used.The stem performs self-attention within each 4×4 block of the original image, followed by batch normalization and a 4×4 max pool operation. Results are below : images

Coco Object Detection

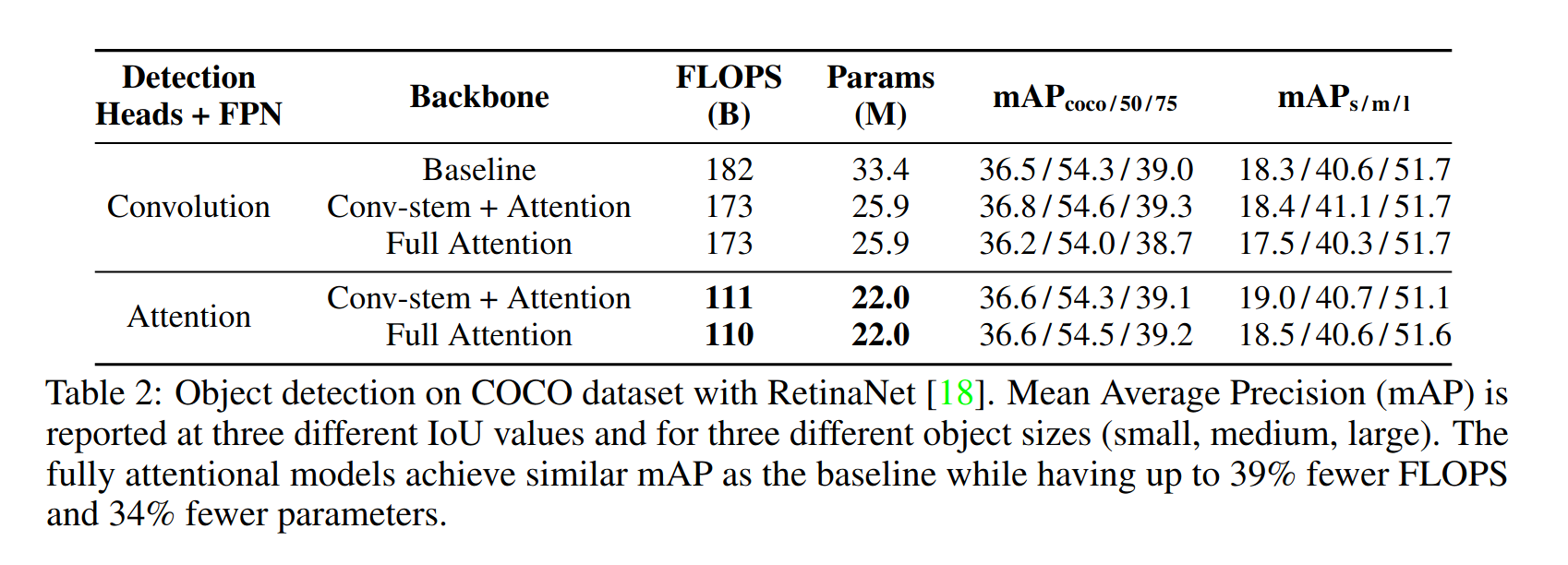
Here Retina Net is used with a classification backbone, followed by an FPN, the network has 2 detection heads. Results are in the table below : images

We can see that using attention based backbone we can achieve results on par with a conv backbone, but with 22% less parameters. This can be extended by additionaly making the FPN and the detection heads attention-based and thereby reducing paraneter count by 34% and more importantly FLOPS by 39%.

Where is stand-alone attention most useful ?

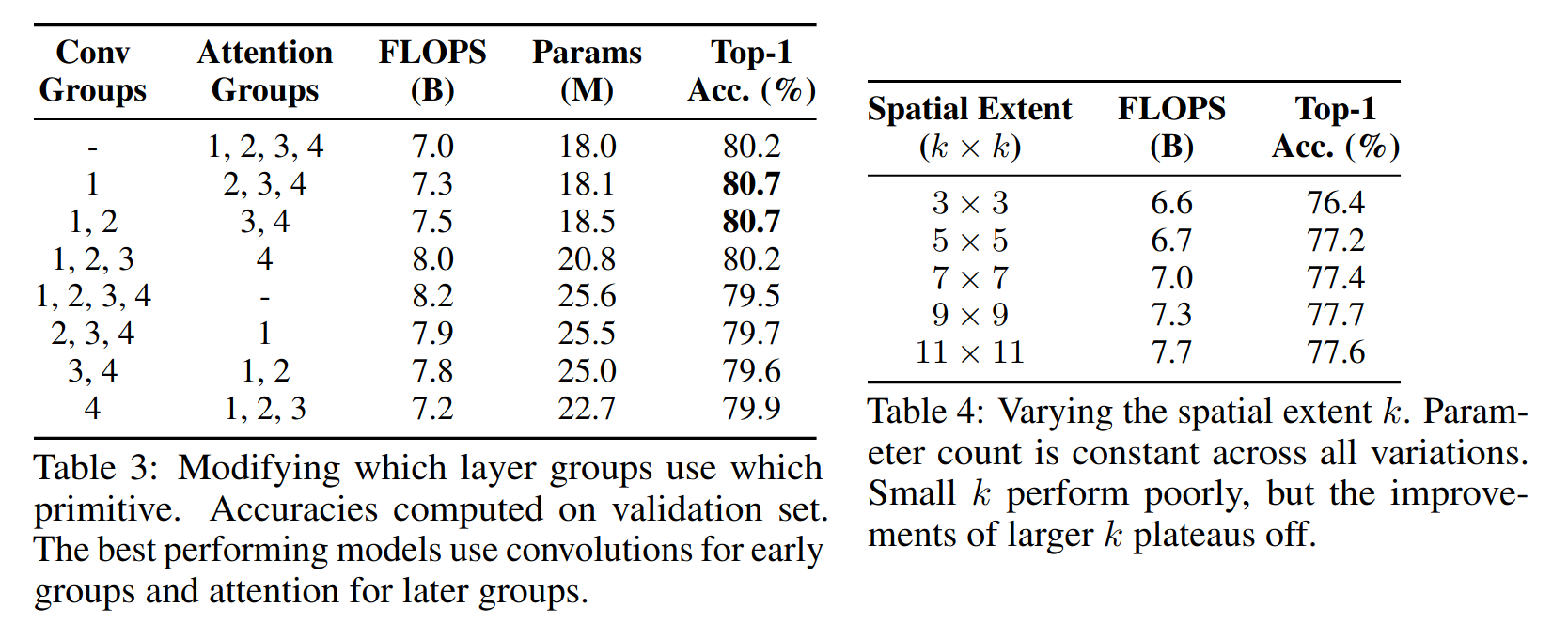
images

Results are schown in the tables above.

Stem

The basic results for the stem is that, convolutions perform very well here, as described above self-attention can not easily learn edges due to the high spatial correlation which is captured very well by conv layers though.

Full Net

The authors basically state what has been described above, conv layers capture low level features very well, while attention is able to model global relations effectively. Therefore an optimal architecture should contain both attention and convolutional layers.

Which attention features are important ?

Effect of spatial extent of self-attention (Table 4) : The value of spatial extent k should generally be larger (for example k=11), the exact optimal setting depends on hyperaparameter choices.
Importance of positional information (Table 5 + 6) 3 types of encoding were used : no positional encoding, sinusodial encoing and absolute pixel position. Relativ encoding performs 2% better than absolute one. Removing content-content interaction only descreases accuracy by 0.5%. Therefore the positional encoding seems to be very important and can be a strong focus of their future research.
Importance of spatially-aware attention stem (Table 7) Using stand-alone attention in the stem with spatially-aware values, it outperforms vanilla stand-alone attention by 1.4%, while having similar FLOPS. Using a spatial convolution to the values instead of spatially-aware point-wise transformations (see above), leads to more FLOPS and slightly worse results. A future goal of the authors is to unify attention used across the stem and main