What did the authors want to achieve ?

In recent years, a lot of different first order methods (ADAGRAD, RMSProp, ADAM, AMSGRAD) have been introduced for training deep neural nets in order to combat the uniform gradient scaling of SGD and it's slower training speed. Experiments and the release of state of the art CV and NLP models - which use traditional SGD (often with momentum) - prove that these optimizers generalize poorly in comparison to classic SGD. Sometimes they don't even converge, which is largely because of unstable and extreme learning rates.

The authors therefore provide new, dynamically bounded versions of AMSGRAD and ADAM, called AMSBOUND and ADABOUND. These new techniques can be seen as adaptive methods during early training, which smoothly transform into SGD/SGD with momentum as training time increases. Their method is inspired by gradient clipping.

Methods

Analysis of already existing adaptive methods

The figure above shows the generic training loop that was used by the authors, where :

$g_{t}$ represents the gradient at step $t$
$\alpha_{t}$ represents the learning rate at step $t$, which is gradually being reduced for theoretical proof of convergence
$m_{t}$ represents the momentum term at step $t$, a function of the gradients
$V_{t}$ represents the scaling term at step $t$, a function of the gradients

The table above shows different optimizers w.r.t to the generic training loop. $\phi_{t}$ and $\psi_{t}$ are the respective functions used for computing $m_{t}$ and $V_{t}$ respectively.

The authors mainly focus on ADAM in their research, as it is very general so it also applies to other adaptive methods (RMSProp, ADAGRAD). Note that ADAM is a combination of RMSprop and momentum, with the distinction that momentum is incorporated directly in the first-order moment estimate (with the use of exponential weighting) and also the additional use of weight decay.

At the time of writing, AMSGRAD was a recently released adaptive method, which was supposed to perform as well as SGD. However AMSGRAD does not yield evident improvement when compared to ADAM. AMSGRAD uses a smaller learning rate than ADAM and the AMSGRAD researchers consider that large learning rates are probLematic. Due to the smaller learning rate being used in AMSGRAD, the authors suspect that small learning rates might be a problem for ADAM as well.

To prove their theory, the authors sample learning rates of several weights and biases for ResNet-34 on CIFAR-10 with ADAM. They randomly select 9 3x3 conv kernels from different layers and biases from the last fully connected layer. Because parameters of the same layer very similar, 9 weights sampled from 9 kernels and one bias are considered. These weights and the bias are visualized in a heatmap. They find that tiny learning rates of smaller than 0.01 and larger ones greater than 1000 lead to the model being closer to convergence. Therefore it is empirically proven, that the learning rate can be both too large and too small in extreme cases. AMSGRAD combats the impact of large learning rates, but it does neglect the other side of the spectrum.

In a second experiment, the authors consider a set of linear functions with different gradients. In their example (see Page 4, upper part of the page), once every $C$ steps a gradient of -1 (moves into the wrong direction) occurs and at the next step a gradient of 2 occurs. Even though 2 is larger than 1 in terms of the abolute value, the larger gradient can not counteract the -1 gradient as the learning rate is scaled down in this later time step leading to x diverging.

3 theorems formalize the intuition :

Theorem 1

There is an online convex optimization problem where for any initial step size α, ADAM has non-zero average regret. (ADAM does not converge) This problem does not occur with SGD, as for a large amount of possible choices for α, the average regret for SGD converges to 0. This is mostly a problem at the end of training, where a lot of gradients are close to zero and the average of 2n order momentum is very various beacuse of the exponential moving average. In this case correct signals occur rarely, which may lead to the algorithm not being able to converge (refer to the example with the gradients of -1 and 2 earlier). Their results show that for any case where $\beta_{1} < \sqrt{\beta_{2}}$ , ADAM does not converge regardless of the step size. Note the standard values are usually $\beta_{1}=0.9$ and $\beta_{2}=0.999$, which proves that $\beta_{1} < \sqrt{\beta_{2}}$, because $0.9 < 0.9995$.

Theorem 2

Refers to the earlier point, that there is an online convex optimzation setting, where ADAM does not converge when $\beta_{1} < \sqrt{\beta_{2}}$ for $\beta_{1}$,$\beta_{2}$ $\in [0,1)$

Theorem 3

Just like theorem 2, but in a stochastic convex optimization setting : There is a stochatic convex optimzation setting, where ADAM does not converge when $\beta_{1} < \sqrt{\beta_{2}}$ for $\beta_{1}$,$\beta_{2}$ $\in [0,1)$

By formulating these 3 theorems, it is proven that the impact of extreme learning rates will lead to a lacking generalization ability and will not be able to solve the problem.

Adabound

As mentioned in the beginning of the paper, the goal should be to achieve SGD performance with ADAM training speed.

The above algorithm is essentially ADAM with clipping in order to constrain the learning rate to be in $[\eta_{l},\eta_{u}]$. For ADAM $\eta_{l} = 0$ and $\eta_{u} = \infty$ and for SGD(optionally with Momentum) with a learning rate $\alpha$, $\eta_{l} = \eta_{u} = \alpha$. The bound are functions of step $t$, with the lower bound $\eta_{l}(t)$ is a non-decreasing function that starts from zero and converges to SGD's $\alpha$ and the upper bound $\eta_{u}(t)$ being a function that starts from $\infty$ and converges to $\alpha$ as well. The functions are : $\eta_{l}(t) = 0.1 - \frac{0.1}{(1-\beta_{2})t + 1}$
$\eta_{u}(t) = 0.1 + \frac{0.1}{(1-\beta_{2})t}$

We therefore reach the SGD state in the end as bound become increasingly restricted with higher step size $t$. The authors empasize that this method is better than using a mixed ADAM and SGD approach with a "hard switch" (Kesker & Socher 2017) which also introduces a hard to tune hyperparameter. The result is proven for Adabound in theorem 4, which also shows that ADABOUND is upper bounded by $O(\sqrt{T})$ :

The authors provide extensive and very understandable proofs in their appendix.

Implementation

An implementation of ADABOUND and ADABOUNDW by the authors can be found here. We can see that the implementation is very similar to the standard ADAM optimizer in the Pytorch source code. The difference is the if/else condition in the end which keeps track of the maximum 2nd moment running average, as well as the bounding at the end of the step function. ADABOUNDW also adds weight decay at the end.

Results

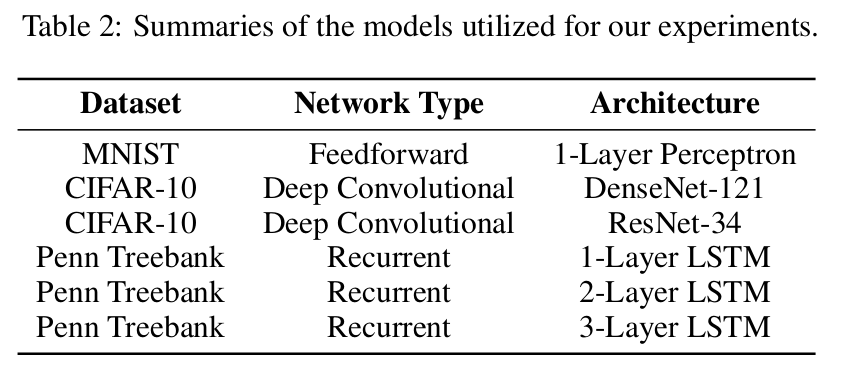
The authors compare ADABOUND and AMSBOUND to ADAM, AMSGRAD, ADAGRAD and SGD on the tasks above with the respective architectures. Hyperparameters are tuned for each optimizer seperately using a logarithmic grid which can be extrapolated if an extreme value is determined to perform the best.

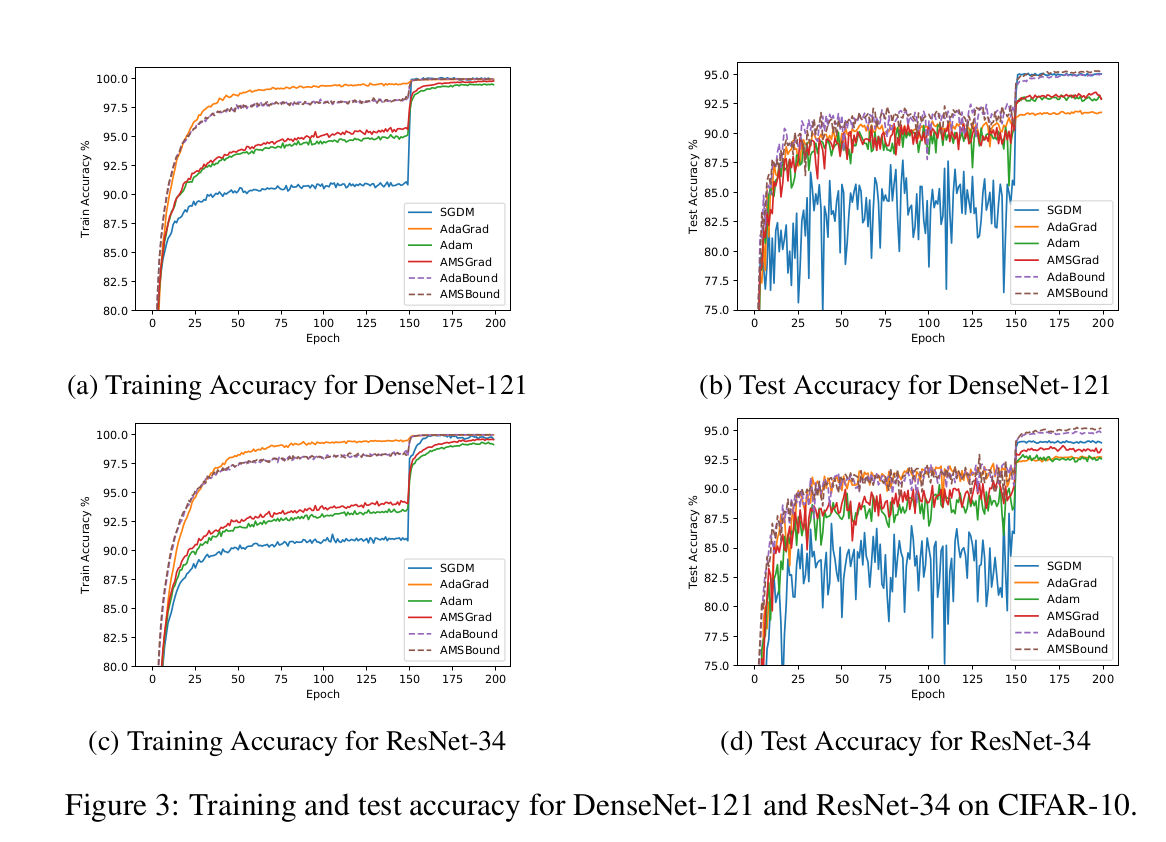
The above diagrams show the performance of ADABOUND/AMSBOUND when compared to traditional methods. With DenseNet-121 on CIFAR-10 ADABOUND is about 2% better than it's base methods during test. With ResNet, they even outperform SGD (with momentum) @ test time by 1%. Much more improvment in deep conv nets is oberved when compared to perceptrons.

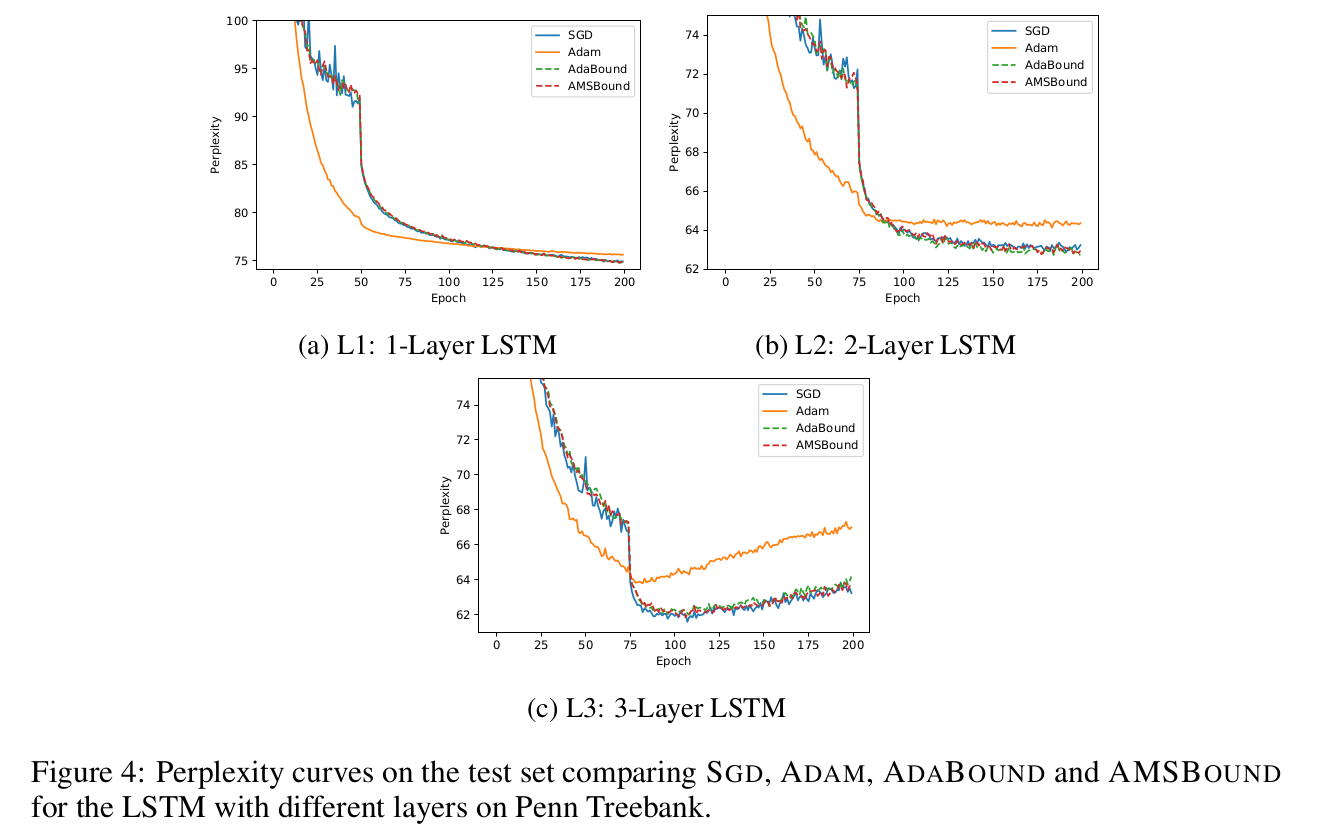
For RNNs ADAM does have the best initial progress but stagnates very quickly, with AMSBOUND/ADABOUND being smoother than SGD (with momentum). Compared to ADAM it outperforms it by 1.1% in the 1 layer LSTM case and 2.8% in the 3 Layer case. This further proves that increasingly more complex architectures benefit even more from AMSBOUND/ADABOUND. This is due to extreme learning rates being more likely to occur with complex models.

The authors summarize that while AMSBOUND/ADABOUND perform well with complex architectures, there is still potential for shallower architectures. It is also unclear why SGD performs so well in most cases. Other ways for improvment should also be considered, the authors propose weight decay as a potential often (AMSBOUNDW).