Paper Link

What did the authors want to achieve ?

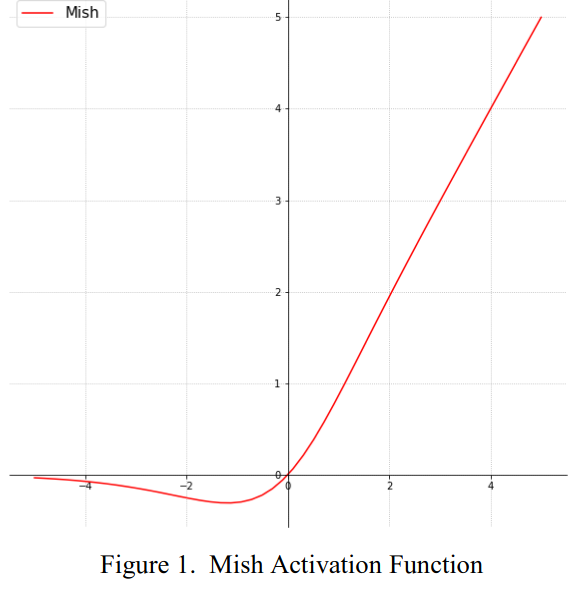
Propose a new activation function which replaces upon the known standards such as ReLU and Swish. The function proposed is called Mish activation and is defined by : $f(x) = x * tanh(softplus(x))$ Recall that Sofplus is defined as $f(x) = ln(1+e^{x})$ The authors show that it can be more effective than ReLU and Swish for Computer Vision tasks. images

Methods

Mish Activation

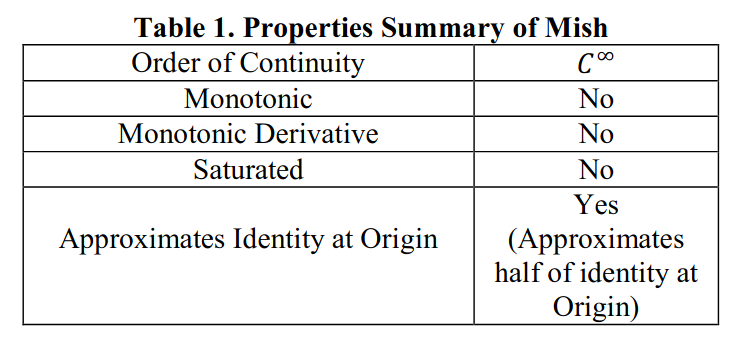
As explained in the intro, Mish is a novel activation function. It is inspired by ReLU and Swish and has a bounded bottom value of $~ -0.31$
The derivative is defined as : $f^{'}(x) = \frac{e^{x} * w}{\delta^{2}}$
With $w=4*(x+1) + 4e^{2x} + e^{3x} +e^{x} * (4x+6)$
and $\delta = 2e^{2x} + e^{2x} + 2$
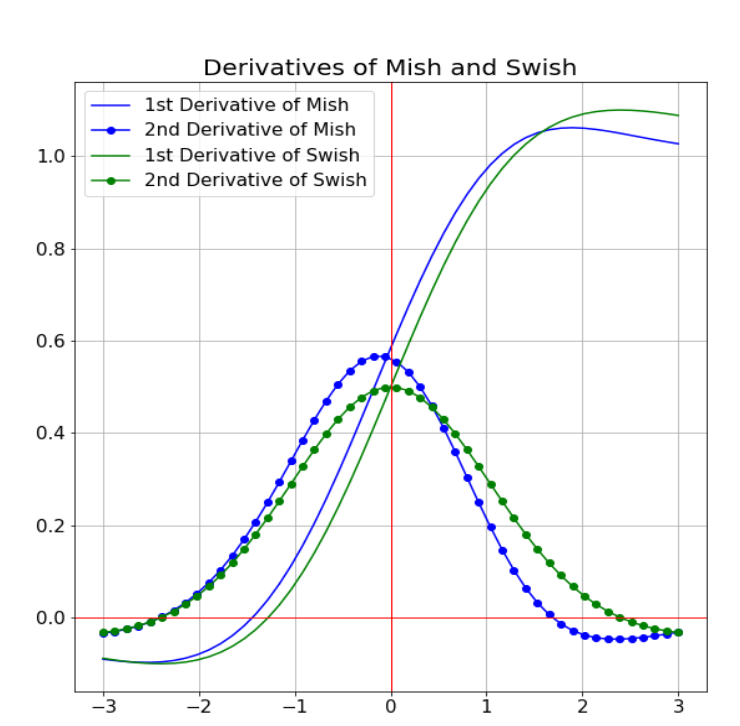
It also has a self gating property, which means that it simply takes a scalar as input and allows it to easily replace ReLU in existing networks. A plot including Mish and Swish derivatives is shown below : images

Code

We can implement Mish in Pytorch the following way :

class MishImplementation(torch.autograd.Function):
    @staticmethod
    def forward(ctx,x):
        ctx.save_for_backward(x)
        return x.mul(torch.tanh(F.softplus(x)) # x * tanh(ln(1 + exp(x)))
   @staticmethod
   def backward(ctx,grad_output):
        x = ctx.saved_tensors[0]
        sx = torch.sigmoid(x)
        fx = F.sofplus(x).tanh()
        return grad_output * (fx + x * sx * (1 - fx * fx))

Credits go to the author of the paper and the implementation above that is used in YOLOv3 by Ultralytics.

Explanation

image The authors explain why Mish does improve upon current results in this section and emphasize the advantageous properties of Mish.

Like Relu and Swish, Mish is unbounded above, which prevents saturation and therefore vanishing gradients. The about -0.31 bound below adds strong regularization properties. Not killing gradients when x is below 0 improves gradient flow and therefore improves expressivity. Famously ReLU is not differentiable at 0, the smoothness of Mish makes it continuously differentiable. The smoother function allow for smoother loss functions and therefore better optimization. The authors summarize these properties and the table above.

The authors generally recommend to use a higher amount of epochs with Mish activation. This obviously introduces some overhead during training.

Results

Hyperparameter study

The author studies the difference between ReLU, Swish and Mish in Section 3.1 by considering fully connected nets with different layer amounts batch norm, dropout and no residual connections, plots are shown for every category. The most important takeaway is that Mish is better than current SOTA for optimizing larger and wider networks. It has to be criticized that the author is not using residual connections here, as this might increase the advantage of Mish even more than it would in a real setting with a skip connection network. They also show that larger batch sizes benefit from Mish, it is also more stable for different initalizations and slightly more robust to noise.

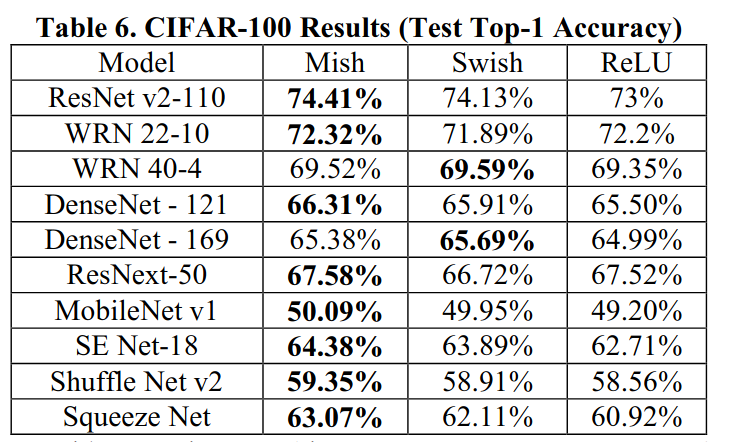
The results are replicated in experiments with a 6-layer CNN. Here Mish outperforms Swish with 75.6% to 71.7% on CIFAR-100. Swish did not seem to learn for the first 10 epochs here due to dead gradients.

The author also shows that Mish outperforms Swish when using Cosine Annealing and outperforms Swish by about 9% when using Mixup with $\alpha=0.2$ to compare the two methods.
Statistical comparison shows that Mish has highest mean test accuracy and lowest mean standard deviation when compared to ReLU and Swish.

It is also mentioned that Mish is slightly less efficient on GPU than the other two mentioned activation functions.

Different Architectures with Mish

The author compares Mish by training with different networks and soley replacing ReLU/Swish with Mish, while leaving the hyperparameters unchanged. The superior performance of Mish during CIFAR100 can be seen in the table below : image