SE Net Summary
Squeeze and Excitation Blocks to improve existing ARchitectures with close to 0 extra compute cost
SENET Paper Summary
(Jie HU, Li Shen, Samuel Albanie, Gang Sun, Enhua Wu)
What did the authors want to achieve ?
So far most research was focused on the feature hierarchy (global receptive fields are obtained through multi-scale operations, interleaving layers, ...) the authors here want to focus on channel relationship instead. They propose a new blok type called the "Squeeze and excitation block", which models dependencies between channels. They achieve new SOTA results on ImageNet and won the competition in 2017.
Methods Proposed
Squeeze-and-Excitation Block :
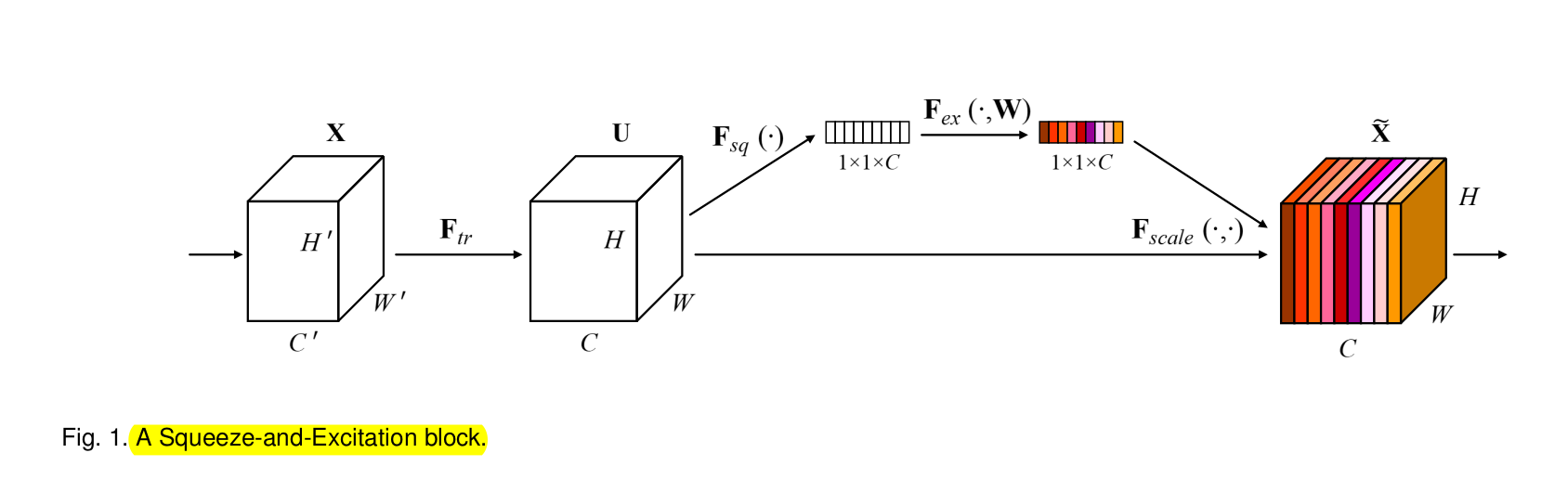
feature maps $U$ are first passed through a $squeeze$ operation, this results in a descriptor. It stacks the maps by it's spatial Dimensions (HxW), so the total size is (HxWxnumber of channels), essentially it produces an Embedding.
After that an $excitation$ operation is applied, it is a self gating mechanism. It uses the emedding as an input and outputs per channel weights. This operation is then applied to the feature maps $U$. SE Blocks can be stacked like Dense blocks, Residual blocks, etc.
In the early layers, SE blocks are class agnostic, while they are very class specific in the later ones. Therfore the advantage feature recalibration can be accumulated in the net.
Squeeze
Each filter only has a local receptive field, which is only focusing on that region. The researchers therefore propose the squeeze operation to create one descriptor of global information. It is generated by shrinking the input $U$ (using global avg. pooling) through it's spatial dimensions :
$z_{c} = F_{sq}(u_{c}) = \dfrac{1}{H*W} * \sum\limits_{i=1}^H \sum\limits_{j=1}^W u_{c}(i,j) $
The output $z$ can be interpreted as a collection of the local descriptors, together they describe the whole image.
Excitation
The excitation block is responsible for capturing channel-wise dependencies. The authors choose a function that is 1) flexibel (learn non-linear interactions between channels) and 2) has a non-mutually exclusive relationship, because they want to have the ability to emphasize multiple channels and thereby avoid using a one-hot activation. The authors propose a gating mechanism to do this :
$s = F_{ex}(z,W) = \sigma(g,(z,W)) = \sigma(W_{2}\delta(W_{1}z))$
Here $\delta$ is the ReLU activation function
$W_{1} \epsilon R^{\frac{C}{R} * C} $
$W_{2} \epsilon R^{C * \frac{C}{R} } $
In order to limit the compute complexity, the authors make the gating mechanism consist of a bottleneck with 2 FC layers around the non-linear activation function. It uses a reduction ration r (for good choice of this refer to 6.1 in the paper), a ReLU and then an increasing layer for dimensionality. The final output is then obtained by rescaling $U$ with an activation (scalar multiplies channel-wise). In a way SE blocks produce their own self attention on channels that are not locally confined, by mapping the descriptor produced by squeeze to channel weights.
SE blocks can be nicely implemented into existing architectures such as Inception, ResNet or ResNeXt blocks. DOW
Compute complexity
Due to the global avg pooling in the squeeze part, only two FC layers and channelwise scaling in the excitation part, only 0.26% inference compute increase compared to a normal ResNet-50 (with image size 224x224) is observed. SE blocks increases ResNet parameter size by about ~10% (2.5 Million parameters).
Results
- the authors prove that Squeeze and Excitation do both improve the performance and can be easily added to most architectures. It yields an improvement independent of architecture, but the exact type of SE block used should be researched depending on the base architecture.
- Later SE layers learn close to the Identity mapping, so
- 2-3% mAP improvement compared to ResNet backbone Faster-RCNN
- 25% improvement on ImageNet top-5 error