Delving Deep into Rectifiers a summary

• Delving Deep into Rectifiers:
  • What did the authors want to achieve ?
  • Key elements
    • PReLU
    • Kaiming Initalization
    • Implementation Details
  • Results and Conclusion

Delving Deep into Rectifiers:

Surpassing Human-Level Performance on ImageNet Classification a summary of the paper

What did the authors want to achieve ?

• Achieve above human level performance on vision (ImageNet)
• Train deep Networks with rectifier functions (ReLu,LReLu,PReLU) effectively
• Improve accuracy by enabling the training of deeper and larger networks

Key elements

• The key elements are a different kind of rectifier activation function called PReLu, which is very similar to LReLu as well as a different initalization technique called Kaiming/He init which improves upon the fact that Xavier initalization does not consider the non-linearities of ReLu kind functions

PReLU

• As we can see PReLu looks a lot like LReLu, having a negative slope a when x < 0, however this slope is not fixed in the beginning but learned by introducing a few hyperparameters
• Due to the number of extra hyperparams being equal to the number of channels, no additional risk of overfitting is introduced
• PReLu seems to keep more information in early layers and becomes more discriminative in deeper stages due to being able to model more non-linear functions

Kaiming Initalization

• The problem with Xavier init, is that it does not take into account the non-linearities of rectifier funcions, therefore a new init technique is derived by taking these activation functions into account, for the forward pass the following is derived :

  • Based on the response of a conv layer, which is computed by : $y_{l} = W_{l}*x_{l}+b_{l}$ ,with $x$ being a $ n = k^{2}*c$ vector ($k*k$ co-located pixels, in $c$ channels) and $W_{l}$ being a $d$ x $n$ matrix, where $d$ is the num of filters

  • The elements in $W_{l}$ and $x_{l}$ are assumed to be independent from each other and share the same distribution, $W_{l}$ and $x_{l}$ are also independet from each other it follows : $Var[y_{l}] = n_{l} *Var[w_{l}*x_{l}] $

  • We let $w_{l}$ have zero mean, the variance of the product of independent variables gives us :
    $Var[y_{l}] = n_{l} *Var[w_{l}]*Var[x_{l}] $ , which leads to $Var[y_{l}] = n_{l} *Var[w_{l}]*E[x_{l}^{2}] $

  • $E[x_{l}^{2}]$ is the expectation of the square of $x_{l}$, we notice that $E[x_{l}^{2}]\neq Var[x_{l}]$ unless $x_{l}$ has 0 mean (Random variability) , which is not the case for ReLu : $x_{l} = max(0,y_{l-1})$

  • if $w_{l-1}$ is symmetric around 0 and $b_{l-1}=0$, it follows that $y_{l-1}$ is a symmetric distribution around zero. This means that $E[x_{l}^{2}]=0.5 * Var[y_{l-1}]$ when the activation is ReLu thus : $Var[y_{l}] = 0.5 * n_{l} *Var[w_{l}]*Var[y_{l-1}] $

  • when we have L layers we have :

    $Var[y_{l}] = Var[y_{1}] * \prod^{L}_{l=2} (0.5 * n_{l} *Var[w_{l}])$

  • the initalization should not magnify the magnitude of the inputs signals, this is achieved by applying a proper scalar :

  $0.5 * n_{l} *Var[w_{l}] = 1, \forall {l}$ (ReLu case)

  $0.5 *(1+a^{2}) * n_{l} *Var[w_{l}] = 1, \forall {l}$ (PReLu case)

=> this distribution is a 0-mean Gaussian with a std of $\sqrt{2/n_{l}}$, which is also adopted in the first layer

• For the backward pass the same function applies, with $n_{l}=k_{l}^{2}*d_{l-1} = k_{l}^{2}*c_{l}$ replaced by $\tilde{n}=k_{l}^{2}*d_{l}$ :

  $0.5 * \tilde{n} *Var[w_{l}] = 1, \forall {l}$ (ReLu)

  $0.5 *(1+a^{2}) * \tilde{n} *Var[w_{l}] = 1, \forall {l}$ (PReLu case)

"This means that if the initialization properly scales the backward signal, then this is also the case for the forward signal; and vice versa. For all models in this paper, both forms can make them converge."

Implementation Details

• The standard hyperparms are as follows :
  • Weight decay is 0.0005
  • Momentum is 0.9.
  • Dropout (50%) is used in the first two fc layers
  • Minibatch size is fixed as 128
  • The learning rates are 1e-2, 1e-3,and 1e-4, and is switched when the error plateaus
  • Number of epochs : 80
  • simple variant of Krizhevsky’s method is used to run Multi-GPUs, the GPUs are synched before the first fc layer to run backprop/forward pass on one of the GPUs (3.8x speedup using 4 GPUs, and a 6.0x speedup using 8 GPUs)
• The PReLU hyperparameters (slopes) are trained with Backprop, the authors proposed the following :
  • no weight decay is used
  • the slopes ai are initialized as 0.25
  • the slopes aiare not constrained, even without regularization aiis rarely larger than 1

Results and Conclusion

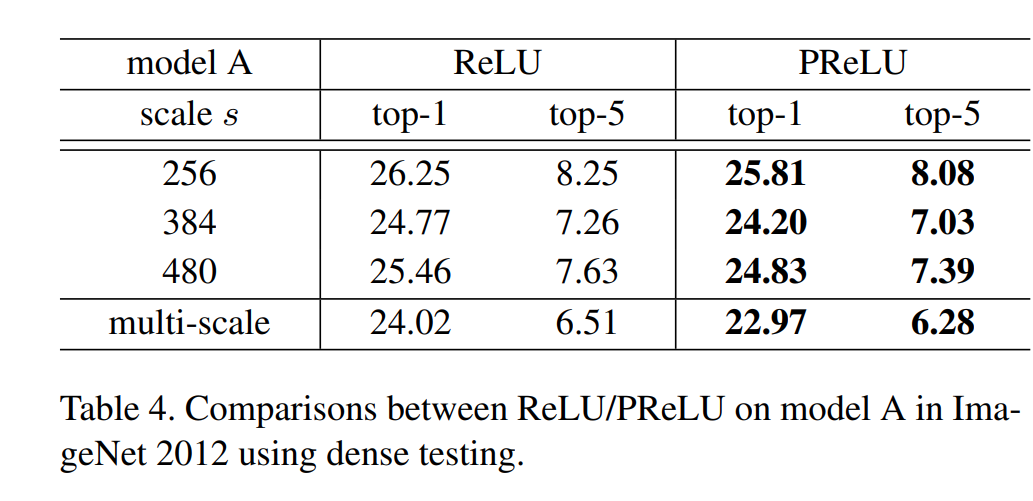
• PRelu reduces top-1 error by 1.05% and top-5 error by 0.23% (@scale 384), when the large model A is used

  

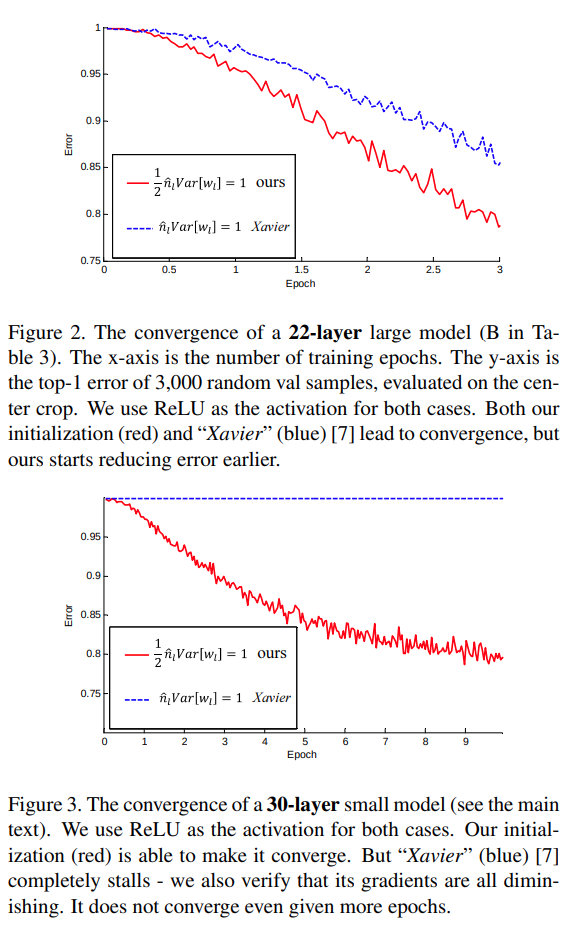
• Kaiming init allows training deep rectifier networks and converges, this allows them to reduce the error to below human level 4.94% compared to 5.1%, you should check out how the human benchmark was established by checking out Andrej Karpathy's blog on this
• It has to be noted however that this is largely due to the fine grained details that can be learned by NNs, if a prediction is incorrect humans still mostly guess the right category (for example vehicle) while NNs can be completely off. So superhuman performance is only achieved in detecting fine grained classes. This can be confirmed when training on the Pascal VOC dataset.